全景解读 LLM 后训练技术

这篇文章是以2025年2月的一篇综述论文为蓝本，对「LLM后训练技术」的全景讲解：[2502.21321] LLM Post-Training: A Deep Dive into Reasoning Large Language Models

引言：从预训练到后训练

2023 年，当 ChatGPT 惊艳世界时，很多人第一次意识到：原来 AI 不仅能背课文，还能写代码、编故事、解数学题。这些聪明表现的背后，得益于大语言模型（LLM）的两个关键训练阶段：预训练（Pretraining）和后训练（Post-training）。

预训练阶段通过海量文本数据（通常达到 TB 级别）的自我监督学习，使模型掌握基本的语言规律和世界知识。但仅有预训练的LLM，就好像刚学会六脉神剑的段誉，一身内功，但不会施展。这时，我们就需要通过「后训练」来给模型能力进行「塑型」—— 通过特定方法让模型在医疗诊断、法律咨询、编程开发等专业领域大显身手，同时学会遵守伦理规范、避免信口开河。正是这些「精装修」步骤，把原始的语言模型变成了我们日常使用的智能助手。

后训练技术的核心价值体现在三个维度：

知识精炼：修正预训练阶段的知识偏差与事实错误
能力对齐：使模型输出符合人类价值观和任务需求
推理增强：赋予模型多步推理、逻辑验证等高级认知能力

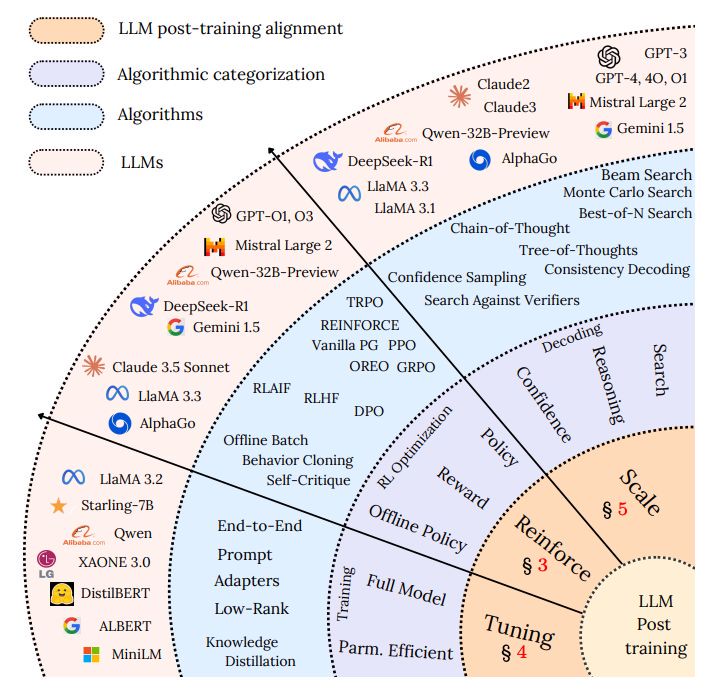
在后面的讲述中，我们沿用上述原论文给出的分类视角（taxonomy），从「微调」、「强化学习」、「测试时拓展」三个类别去认识各种后训练技术。

一、微调技术：模型的定向进化

1.1 全参数微调

全参数微调（Full Fine-tuning）是指在预训练模型的基础上，使用下游任务的数据集，更新模型中的所有参数，以使模型适应特定任务。这种方法在早期的深度学习中非常常见，但随着模型规模的增大，其弊端也逐渐显现。

挑战维度	具体表现	解决方案
计算资源	GPU 内存占用高，训练时间长	参数高效微调 (PEFT)
灾难性遗忘	新任务覆盖旧知识	知识蒸馏 + 持续学习
数据依赖	需要大量标注数据	提示学习 + 数据增强

1.2 参数高效微调 (PEFT)

参数高效微调（Parameter-Efficient Fine-Tuning，PEFT）是一系列旨在以较少的计算资源和数据量，实现与全参数微调相近性能的技术。这类方法通常冻结预训练模型的大部分参数，只训练少量额外的参数。

1.2.1 LoRA 系列技术

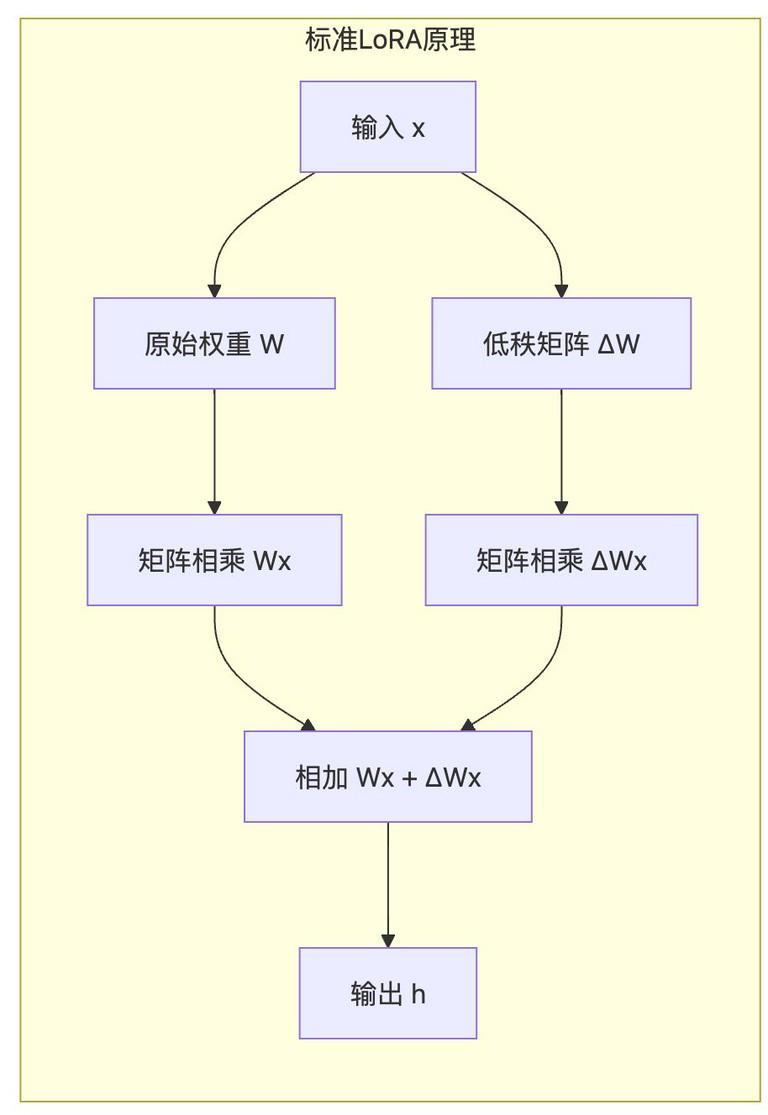
低秩适配（LoRA） 的核心思想是冻结原始参数，通过低秩分解引入可训练参数。

数学原理：

LoRA 假设预训练模型的参数矩阵的更新可以表示为一个低秩矩阵。具体来说，对于一个预训练好的权重矩阵$$W_0 \in \mathbb{R}^{d \times k}$$，LoRA 引入两个低秩矩阵$$A \in \mathbb{R}^{d \times r}$$和$$B \in \mathbb{R}^{r \times k}$$，其中$$r \ll \min(d, k)$$是秩。在微调过程中，只优化$$A$$和$$B$$，而$$W_0$$保持不变。更新后的权重矩阵为：

$$W = W_0 + BA$$

由于$$r$$远小于$$d$$和$$k$$，因此 LoRA 只需要训练很少的参数，就可以达到与全参数微调相近的性能。

伪代码示例：

import torch
import torch.nn as nn

class LoRALayer(nn.Module):
	def __init__(self, in_dim, out_dim, rank):
		super().__init__()
		self.A = nn.Parameter(torch.randn(in_dim, rank))
		self.B = nn.Parameter(torch.zeros(rank, out_dim))
		self.rank = rank #  秩的大小
	def forward(self, x):
		return x @ (self.A @ self.B)  # 低秩矩阵乘积

关键技术演进：

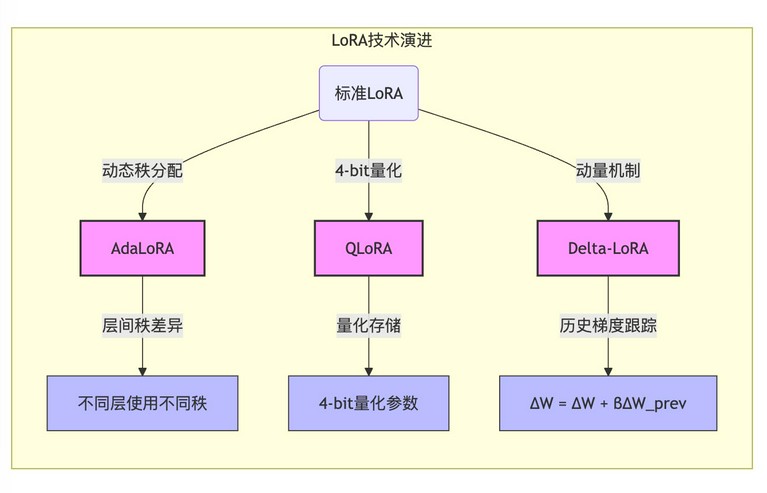
AdaLoRA：
- 核心思想：AdaLoRA（Adaptive LoRA）旨在动态调整各层的秩分配。
- 实现方式：AdaLoRA 通过一些指标（例如，梯度范数）来评估不同层的重要性，并根据重要性动态地调整 LoRA 的秩。更重要的层分配更高的秩，从而获得更好的性能。
QLoRA：
- 核心思想：QLoRA（Quantized LoRA）将4-bit 量化与 LoRA 相结合，以进一步降低显存占用。
- 实现方式：QLoRA 首先将预训练模型的权重量化为 4-bit 精度，然后在此基础上应用 LoRA。由于 4-bit 量化可以显著降低显存占用，因此 QLoRA 可以在有限的 GPU 资源上微调更大的模型。
- 显存节省：QLoRA 可以节省高达 70% 的显存。
Delta-LoRA：
- 核心思想：Delta-LoRA 引入参数更新量的动量机制。
- 实现方式：Delta-LoRA 在更新 LoRA 参数时，考虑之前的更新方向和幅度，从而更稳定地进行微调。

1.2.2 提示微调技术

提示微调（Prompt Tuning） 是一种通过设计合适的提示（Prompt） 来引导预训练模型完成下游任务的技术。与全参数微调和 LoRA 不同，提示微调通常不直接修改预训练模型的参数（注意不是完全不修改参数），而是通过优化提示相关的向量来调整模型的行为。

核心思想：

人工设计到可学习：提示工程（Prompt Engineering）经历了从人工设计提示到可学习提示的演进过程。
利用预训练知识：通过优化提示，引导模型利用预训练知识，从而减少对标注数据的依赖。

数学原理：

公式

$$h_{prompt} = [P_1;P_2;…;P_k] \quad P_i \in \mathbb{R}^{d}$$

描述了可学习的提示向量。其中，$$h_{prompt}$$表示提示向量，$$P_i$$表示第$$i$$个可训练的提示向量，$$k$$表示提示的长度，$$d$$表示提示向量的维度。

位置选择策略：

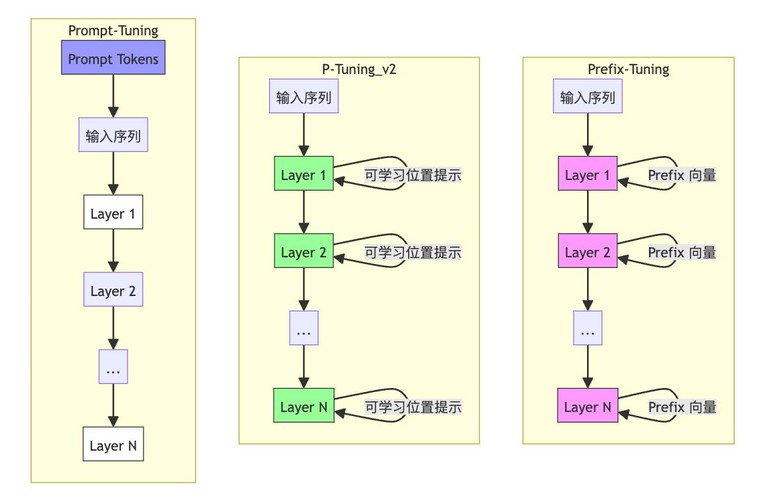
Prefix-Tuning（粉色）：
- 核心思想：只在每层的开头插入可训练的提示向量。
- 数学形式：$$h^{l} = \text{Transformer}([\text{Prefix}^l; x^{l}])$$
- 参数量：每层新增参数$$d \times r$$（$$d$$为维度，$$r$$为前缀长度）
- 优点：Prefix-Tuning 可以有效地影响模型的每一层，从而更好地调整模型的行为。
- 缺点：Prefix-Tuning 需要插入大量的提示向量，可能会增加计算成本。
P-Tuning v2（绿色）：
- 核心思想：分层插入位置可学习。
- 实现方式：P-Tuning v2 首先将提示向量插入到不同的层中，然后通过训练来确定每个提示向量的最佳位置。
- 数学形式：$$\text{Position}^l = \text{softmax}(W_p^l \cdot x^l)$$
- 优点：P-Tuning v2 可以更灵活地调整提示向量的位置，从而更好地适应不同的任务。
Prompt-Tuning（蓝色）：
- 核心思想：仅在输入层添加可训练提示词。
- 参数量：仅需$$k \times d$$（$$k$$为提示词数量）
- 数学形式：$$h = \text{LM}([\text{Prompt}; x])$$
- 优点：Prompt-Tuning 的实现简单，计算成本低。
- 缺点：Prompt-Tuning 的效果可能不如 Prefix-Tuning 和 P-Tuning v2。

关键差异对比表：

维度	Prefix-Tuning	P-Tuning v2	Prompt-Tuning
插入位置	每层输入序列头部	每层可学习位置	仅输入层头部
可训练参数占比	0.5%-2%	0.3%-1.5%	0.01%-0.1%
典型应用场景	复杂逻辑推理	多任务适配	轻量化快速部署
显存占用	高（需存储各层前缀）	中	极低
训练速度	慢（需反向传播至各层）	中等	快（仅输入层梯度）

技术演进趋势：

动态混合提示作为最新发展方向，允许模型自主决定：

是否需要在某层插入提示
最佳提示插入位置
不同提示向量的权重分配

1.3 领域自适应微调

领域自适应微调（Domain Adaptive Fine-Tuning） 是指在特定领域的数据上对预训练模型进行微调，以使其更好地适应该领域的任务。这种方法在医疗、法律等专业领域尤其重要，因为这些领域的数据具有独特的特点和术语。

案例：医疗问答系统的微调策略

以一个医疗问答系统的微调策略为例：

数据构造：
- 混合通用指令数据 (20%) + 专业文献问答 (80%)：
  - 通用指令数据：例如，”请解释什么是高血压？”、”如何预防感冒？” 等。这些数据可以帮助模型保持通用的语言理解能力。
  - 专业文献问答：从医学文献中提取问题和答案，例如，”《柳叶刀》杂志最近发表了关于 COVID-19 疫苗有效性的研究，请总结其主要发现。”。这些数据可以帮助模型学习专业的医学知识。
  - 比例：混合比例的选择需要根据实际情况进行调整。一般来说，如果领域数据比较稀缺，可以适当增加通用指令数据的比例。
分层微调：
- 计算效率：只微调部分层可以显著降低计算成本。
- 避免灾难性遗忘：冻结大部分层可以保留预训练模型的通用知识，从而避免灾难性遗忘。
- 微调后 10% 的原因：这是一个经验性的选择，通常认为后几层更接近特定任务，因此微调这些层可以更好地适应领域数据。
- 需要实验验证：最佳的微调层数需要根据实际情况进行实验验证。
评估指标：
- FActScore（事实一致性评分）> 0.85：
  - FActScore：一种用于评估模型生成答案的事实一致性的指标。FActScore 越高，表示模型生成的答案与事实越一致。
  - 重要性：在医疗领域，事实一致性至关重要。如果模型生成错误的医疗信息，可能会对患者的健康造成严重影响。

二、强化学习：从对齐到推理

2.1 LLM推理技术全景图

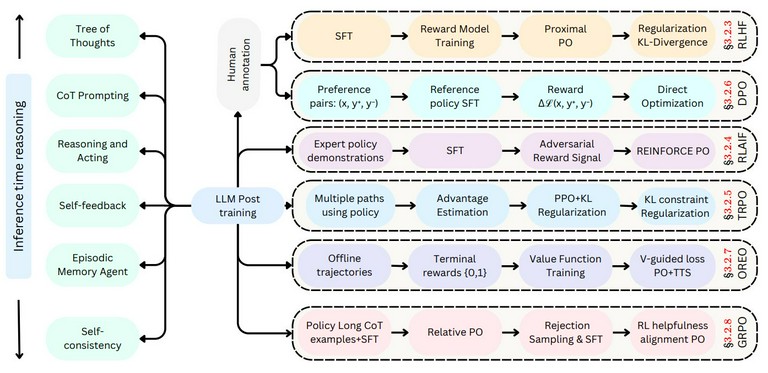
2.2 奖励建模

奖励建模（Reward Modeling） 是很多 RL 方法的关键步骤之一。它的目标是根据人类的偏好数据，训练一个能够预测人类对模型输出的偏好程度的模型。

偏好数据：训练奖励模型需要大量的偏好数据。这些数据通常由人工标注，例如，让人类对不同的模型输出进行排序或打分。
奖励模型的选择：奖励模型可以是任何一种机器学习模型，例如，线性模型、神经网络等。常见的选择是使用与预训练语言模型结构相似的模型。

Bradley-Terry 模型是一种常用的奖励建模方法：假设对于给定的输入$$x$$，人类更喜欢输出$$y_i$$而不是$$y_j$$的概率可以表示为：

$$P(y_i \succ y_j|x) = \frac{\exp(R(x,y_i))}{\exp(R(x,y_i)) + \exp(R(x,y_j))}$$

其中，$$R(x, y)$$是奖励模型给出的奖励值，表示模型认为输出$$y$$对于输入$$x$$的好坏程度。$$\succ$$表示偏好关系，即$$y_i \succ y_j$$表示人类更喜欢$$y_i$$而不是$$y_j$$。

训练目标

训练奖励模型的目标是最小化负对数似然：

$$\mathcal{L}_{BT} = -\sum \log P(y_i \succ y_j|x)$$

这个公式表示，我们希望奖励模型给出的奖励值能够尽可能地符合人类的偏好。也就是说，如果人类更喜欢$$y_i$$而不是$$y_j$$，那么我们希望$$R(x, y_i)$$尽可能地大于$$R(x, y_j)$$。

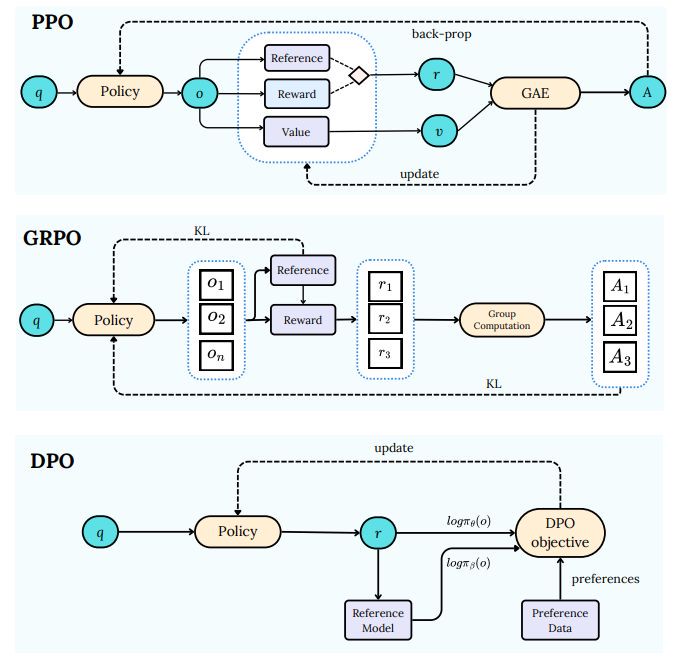
2.3 主流优化算法对比

方法	更新机制	优势	局限
PPO	带约束的策略梯度	训练稳定	需要价值函数估计
DPO	直接偏好优化	无需奖励模型	依赖高质量偏好数据
GRPO	组相对策略优化	降低方差	需要并行采样多个响应

2.4 过程奖励 Vs 结果奖励

在强化学习中，奖励函数的设计至关重要。奖励函数定义了模型在不同状态下应该获得的奖励，从而引导模型学习到期望的行为。

根据奖励的来源，可以将奖励分为过程奖励和结果奖励。

过程奖励（Process Reward）

过程奖励是指在每个步骤中，根据模型的行为给出的奖励。过程奖励可以提供更密集的反馈信号，帮助模型更快地学习。但缺点是设计比较困难，需要对任务有深入的理解。

举个例子：

def calculate_step_reward(response):
	# 1. 语法正确性检查
	syntax = check_syntax(response)
	# 2. 逻辑连贯性评估
	coherence = model.predict_coherence(response)
	# 3. 事实一致性验证
	fact_check = retrieve_evidence(response)
	return 0.3*syntax + 0.5*coherence + 0.2*fact_check

在这个例子中，奖励函数考虑了三个方面：

语法正确性检查：检查模型生成的文本是否符合语法规则。例如，可以使用语法分析器来判断文本是否存在语法错误。
逻辑连贯性评估：评估模型生成的文本是否逻辑连贯。例如，可以使用语言模型来预测文本的连贯性。
事实一致性验证：验证模型生成的文本是否与事实相符。例如，可以使用知识库来检索相关信息，然后判断模型生成的文本是否与知识库中的信息一致。

对这三个方面进行加权求和，得到最终的奖励值。权重的选择需要根据实际情况进行调整。一般来说，更重要的方面应该分配更高的权重。

结果奖励（Outcome Reward）

结果奖励是指在任务完成后，根据模型的最终结果给出的奖励。结果奖励的设计比较简单，只需要关注最终结果即可。但可能提供较稀疏的反馈信号，导致模型学习困难。典型应用场景包括：

数学问题：最终答案正确性。例如，如果模型生成的答案与正确答案一致，则给出正奖励；否则，给出负奖励。
代码生成：通过单元测试的比例。例如，如果模型生成的代码能够通过所有的单元测试，则给出正奖励；否则，给出负奖励。
对话系统：用户满意度评分。例如，如果用户对模型的回复感到满意，则给出正奖励；否则，给出负奖励。

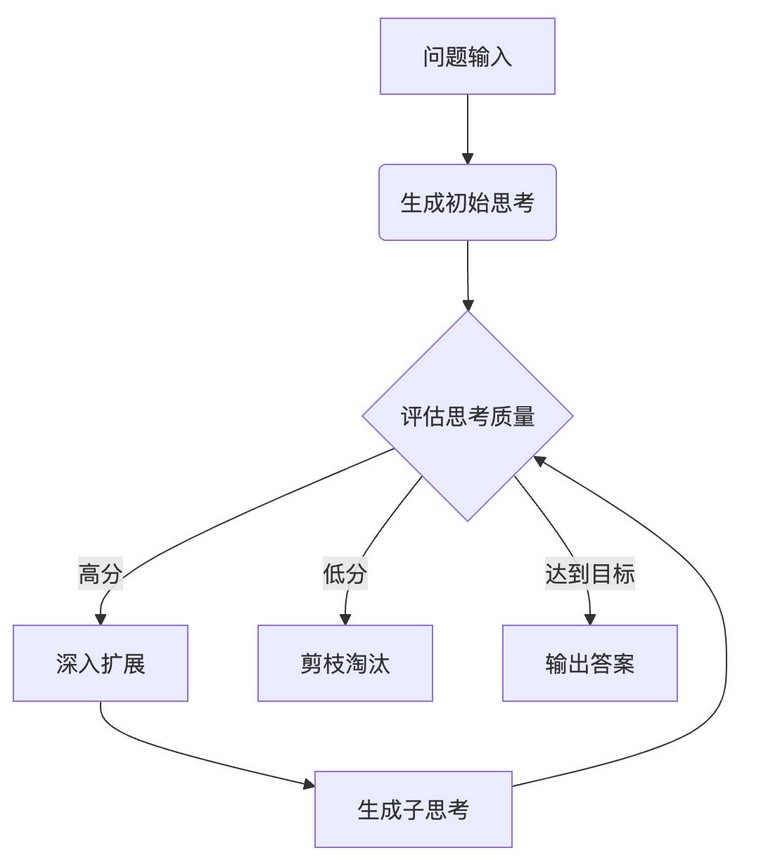
2.5 强化学习的推理增强实践

举一个 思维树（ToT）算法框架 的例子：

思维生成：基于当前状态生成候选思考
状态评估：使用价值函数评估每个候选
广度优先搜索：保留 top-k 候选继续扩展
回溯更新：反向传播累积奖励

三、测试时扩展：推理即搜索

3.1 主流推理增强技术

方法	核心思想	适用场景
链式思考（CoT）	显式生成推理步骤	数学解题、逻辑推理
自洽性解码（SC）	多路径投票机制	开放域问答
思维树（ToT）	树形结构空间搜索	复杂规划问题
蒙特卡洛树搜索（MCTS）	模拟 - 评估 - 回溯机制	游戏类、策略性问题

3.2 计算最优扩展策略

不同的推理增强技术适用于不同的场景。如何根据具体的问题选择最优的推理增强技术呢？这就是 计算最优扩展策略 要解决的问题。

动态计算分配算法 的核心思想是根据问题的难度动态地分配计算资源。对于简单的问题，可以使用简单的推理方法；对于复杂的问题，可以使用更复杂的推理方法。

伪代码示例：

def dynamic_compute_allocation(query):
	difficulty = estimate_difficulty(query)
	if difficulty < 0.3:
		return greedy_decode()
	elif 0.3 <= difficulty < 0.7:
		return beam_search(width=3)
	else:
		return monte_carlo_tree_search(depth=5)

在这个例子中，estimate_difficulty 函数用于评估问题的难度。根据问题的难度，选择不同的推理方法。

如何评估问题的难度呢？一个思路是根据问题的特征来预测。比如：

问题长度与复杂度：问题越长，复杂度越高，难度越大。
领域专业性指标：问题涉及的领域越专业，难度越大。例如，医学问题的难度通常高于一般问题。
历史正确率统计：如果模型在过去的历史数据中对类似问题的正确率较低，则说明该问题的难度较大。
语义模糊性评分：如果问题存在语义模糊性，则难度较大。例如，”苹果公司最近发布了什么？” 这个问题存在语义模糊性，因为 “发布” 可以指发布新产品、发布财报等。

3.3 验证器增强推理

验证器增强推理 是一种通过使用验证器（Verifier）来检查模型生成的答案的正确性，从而提高推理准确率的技术。

可以构建一个多层验证体系，对模型生成的答案进行多方面的验证。

语法验证器：检查代码/公式语法。例如，可以使用语法分析器来判断代码或公式是否存在语法错误。
逻辑验证器：命题逻辑一致性检查。例如，可以使用逻辑推理引擎来判断命题是否符合逻辑。
事实验证器：知识库检索验证。例如，可以使用知识库来检索相关信息，然后判断模型生成的答案是否与知识库中的信息一致。
安全验证器：有害内容过滤。例如，可以使用有害内容检测模型来判断模型生成的文本是否包含有害内容。

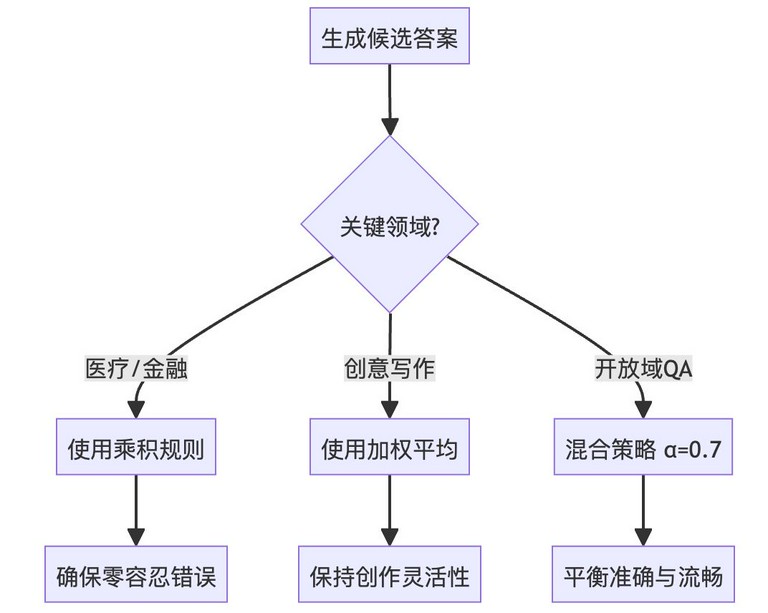
下面这个公式描述了如何将多个验证器的结果组合起来：

$$V_{total} = \prod_{i=1}^n V_i(s) \quad V_i \in [0,1]$$

其中，$$V_{total}$$表示总的验证分数，$$V_i(s)$$表示第$$i$$个验证器对答案$$s$$的评分，$$n$$表示验证器的数量。这个公式表示，总的验证分数是所有验证器评分的乘积。每个验证器的评分都在 0 到 1 之间，评分越高，表示答案越可靠。

乘积的原因：使用乘积的原因是，如果有一个验证器的评分很低，则总的验证分数也会很低，这表示答案的可靠性较低。
其他组合方式：除了乘积之外，还可以使用其他的组合方式，例如，加权平均。

四、挑战与未来方向

4.1 现有技术瓶颈

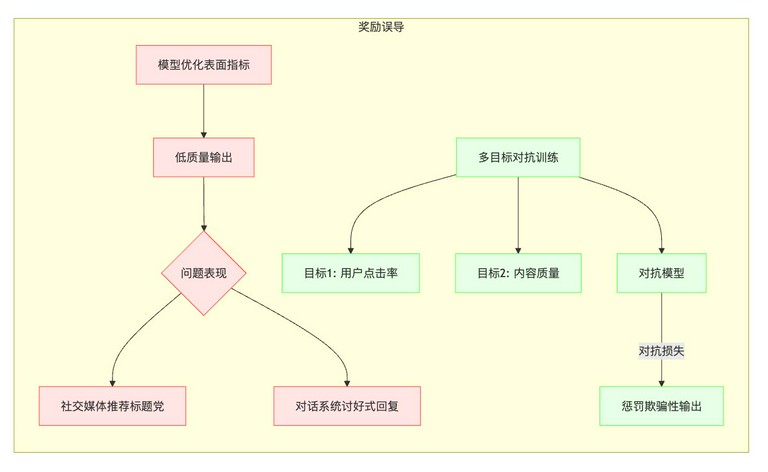
奖励误导（Reward Hacking）

具体挑战：过度优化表面指标。奖励误导是指模型为了获得更高的奖励，采取了一些不符合人类意图的行为。例如，模型可能会生成一些表面上看起来很好，但实际上毫无意义或有害的输出。
示例：
- 社交媒体推荐系统：为了提高用户点击率，模型可能会推荐一些标题耸人听闻、内容低俗的文章，而不是真正有价值的文章。
- 对话系统：为了获得更高的用户满意度评分，模型可能会生成一些讨好用户、但实际上不解决问题的回复。
当前最佳方案：多目标对抗训练。多目标对抗训练是一种通过同时优化多个目标，并引入对抗性损失来防止模型过度优化表面指标的技术。
- 多目标：例如，可以同时优化用户点击率和内容质量。
- 对抗性损失：引入一个对抗模型，用于识别模型生成的欺骗性输出，并惩罚生成这些输出的模型。

长程推理（Long-Range Reasoning）

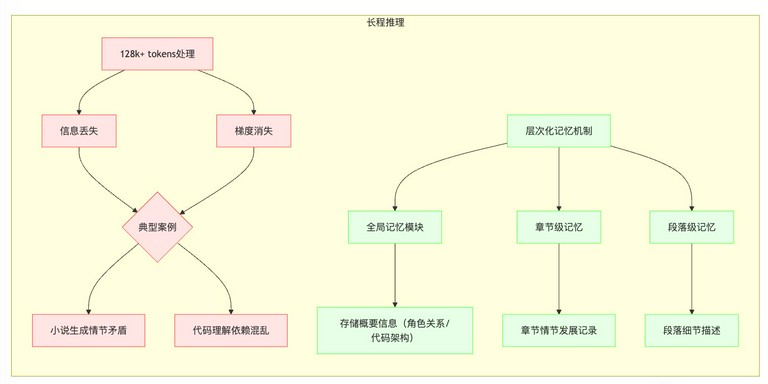
具体挑战：超过 128k tokens 的连贯性。长程推理是指模型在处理长文本时，保持上下文连贯性的能力。由于 Transformer 模型的计算复杂度与序列长度成正比，因此处理长文本的计算成本非常高。此外，模型在长文本中容易出现信息丢失和梯度消失等问题，导致连贯性下降。
示例：
- 小说生成：模型难以生成超过 128k tokens 的连贯小说，因为在长文本中，角色的行为和情节的发展容易出现矛盾。
- 代码理解：模型难以理解超过 128k tokens 的复杂代码库，因为代码中的依赖关系和调用关系非常复杂。
当前最佳方案：层次化记忆机制。层次化记忆机制是一种通过将长文本分解为多个段落或章节，并使用层次化的记忆结构来存储和检索信息的技术。
- 段落或章节：例如，可以将一篇小说分解为多个章节，每个章节包含若干段落。
- 层次化的记忆结构：例如，可以使用一个全局记忆模块来存储整篇小说的概要信息，并使用多个局部记忆模块来存储每个章节的详细信息。

个性化安全（Personalized Safety）

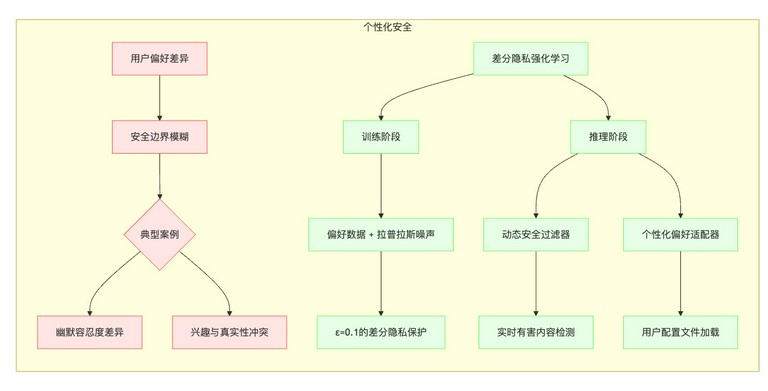
具体挑战：用户特定偏好与通用安全的平衡。不同的用户对安全的定义和容忍度不同。例如，一些用户可能对幽默的容忍度较高，而另一些用户可能认为某些幽默是冒犯性的。如何在满足用户个性化偏好的同时，保证模型的输出是安全的，是一个具有挑战性的问题。
示例：
- 对话系统：如何根据用户的个人喜好，生成既有趣又不会冒犯用户的回复？
- 内容生成：如何根据用户的兴趣，生成既有创意又不会传播虚假信息的文章？
当前最佳方案：差分隐私强化学习。差分隐私强化学习是一种通过在训练过程中添加噪声来保护用户隐私，并在推理时根据用户的偏好进行调整的技术。
- 添加噪声：在训练过程中，向用户的偏好数据中添加噪声，使得模型无法精确地学习用户的偏好，从而保护用户的隐私。
- 根据用户的偏好进行调整：在推理时，根据用户的偏好，对模型的输出进行调整，使其更符合用户的需求。

4.2 前沿研究方向

为了解决上述技术瓶颈，研究人员正在探索一些新的研究方向。比如 元认知机制、物理推理融合 、 群体智能系统等。下面我将对这些方向进行更详细的讲解：

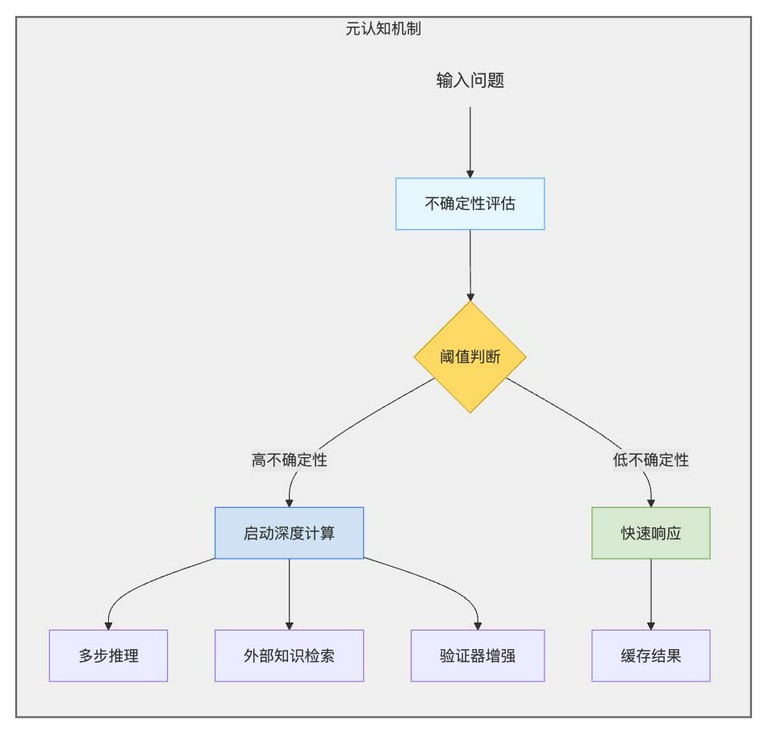
元认知机制（Meta-Cognition）

核心思想是让模型学会何时需要深入思考。元认知是指对认知的认知，即对自己的思考过程的思考。通过赋予模型元认知能力，可以使其能够判断自身是否能够解决当前的问题，并根据需要分配更多的计算资源。

伪代码示例：

def meta_cognition(query):
	uncertainty = calculate_uncertainty(query)
	if uncertainty > threshold:
		return allocate_more_compute(query)
	else:
		return fast_response(query)

在这个例子中，calculate_uncertainty 函数用于评估模型对当前问题的不确定性。如果模型对当前问题的不确定性超过某个阈值，则说明该问题比较复杂，需要分配更多的计算资源（allocate_more_compute）；否则，说明该问题比较简单，可以使用快速响应（fast_response）。

物理推理融合（Physical Reasoning）

核心思想是将符号推理与神经网络结合。物理推理是指模型根据物理定律进行推理的能力。通过将符号推理与神经网络结合，可以使模型既能够利用神经网络的强大表示能力，又能够利用符号推理的精确性和可解释性。

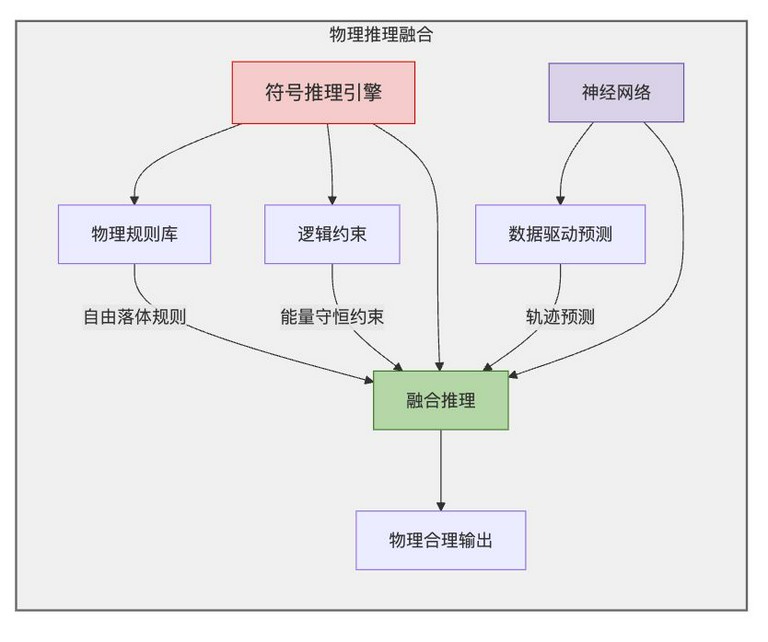
通过将这些物理规则嵌入到模型中，可以使模型能够进行物理推理，例如，预测物体在自由落体运动中的位置和速度。

群体智能系统（Swarm Intelligence）

群体智能是指由多个个体组成的系统，通过个体之间的协作来实现复杂问题的解决。通过构建多模型协作推理框架，可以使不同的模型发挥各自的优势，共同完成复杂的推理任务。

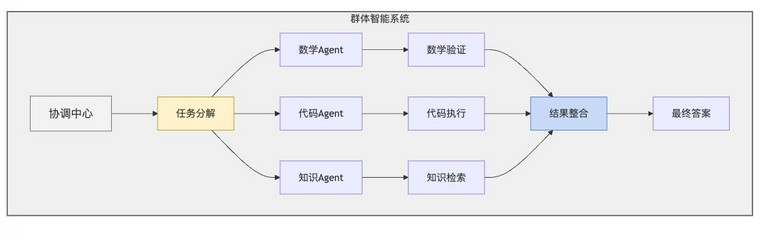
在这个流程图中，「任务分解」Agent 负责将问题分解为多个子问题，并将这些子问题分配给各个子任务Agent。「结果整合」Agent 负责将这些结果整合起来，得到最终的答案。

五、实践指南：如何选择后训练方案

5.1 决策流程图

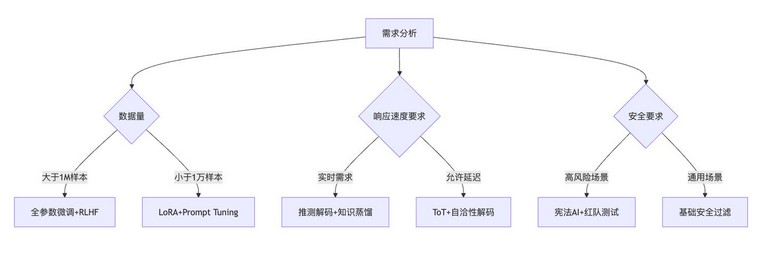
5.2 工具链推荐

工具类型	推荐选项	核心功能
微调框架	HuggingFace PEFT	LoRA/QLoRA实现
RLHF平台	TRL (Transformer RL)	PPO/DPO实现
推理加速	vLLM	分页注意力机制
监控评估	Weights & Biases	训练过程可视化